> INDICE DEL CORSO < Articolo precedente: Sviluppare app multipiattaforma - Le basi: l’algoritmo e il codice (prima parte)
Nel precedente articolo, ho sinteticamente concettualizzato un algoritmo come un’entità che fa qualcosa e, nella pratica quotidiana, questa entità non è altro che un "pezzo" di codice (detto in maniera estremamente grossolana, ma concreta). Ho poi meglio precisato che un algoritmo è un elenco di istruzioni eseguibili da una macchina, in un tempo finito, per fare una determinata cosa. Non tutti i problemi hanno un algoritmo risolutivo, non sempre tra possibili algoritmi diversi per affrontare lo stesso problema è facile capire qual è il migliore e non sempre ci sono indicazioni o documentazione adeguate sui problemi che dobbiamo affrontare.
In questo articolo faremo un primo assaggio del codice, partendo dal caso semplice del calcolo della spazio percorso da un'automobile.
Argomenti:
- Matematica e algoritmi: L’arte perduta di discernere i dati, le incognite e l’algoritmo
- Algoritmi in funzione degli strumenti di cui disponiamo e della logica del linguaggio di programmazione
Matematica e algoritmi: l'arte perduta di discernere i dati, le incognite e l'algoritmo
Ho un caro ricordo delle ore di matematica alle scuole elementari e medie, sia perché parte della matematica, soprattutto quella algebrica, mi ha sempre affascinato (per chi non lo conosce, segnalo il mio sito www.storia-matematica.net), sia perché l’approccio matematico scolastico da me conosciuto è molto in sintonia con il concetto di algoritmo. Ricordo ancora la maestra alle elementari che, per insegnarci come risolvere i problemi di matematica, dopo aver dato la descrizione del problema, procedeva sempre nell’indicarci quali fossero i dati e quali le incognite, prima di iniziare lo svolgimento vero e proprio; da noi bambini e bambine pretendeva la stessa cosa. Anche alle scuole medie il metodo era sempre lo stesso: dati, incognite e svolgimento.
Nel proseguo dei miei studi, però, già alle scuole superiori l’approccio di identificare dati e incognite, di per sé al limite del banale, ma sempre utile per modellizzare i problemi, andava sfumando, per poi sparire completamente all’università, dove non ho mai visto un docente affrontare un problema matematico (o affrontabile con la matematica, ad es. un problema di fisica) identificando per prima cosa quali fossero i dati e quali le incognite. Ognuno aveva il suo approccio, ognuno faceva come meglio gli pareva… peccato, perché una delle principali cause di smarrimento nella risoluzione dei problemi (compresi i problemi di programmazione) è proprio in una modellizzazione sbagliata o in assunzioni sbagliate. In questo senso, nel titolo di questo paragrafo, ho considerato il discernimento di dati, incognite e svolgimento come un'arte perduta.
Per scrivere algoritmi al computer, è meglio procedere come alle scuole elementari. Faccio un esempio pratico.
Problema:
Un'automobile procede alla velocità costante di 108 km/h. Quanti metri percorre in 10 minuti?
Dati:
v = 108 km/h
t = 10 min
Incognite:
s = ? [m]
Svolgimento:
Si tratta di un esempio di moto rettilineo uniforme, in cui vige l'uguaglianza che lo spazio s è uguale alla velocità v moltiplica per il tempo t (a patto di usare correttamente le unità di misura).
La prima cosa che noto è, quindi, che serve un algoritmo che, dati velocità e tempo (input), restituisca lo spazio percorso (output): in questo caso, l'algoritmo è un'espressione matematica.
Entriamo nel vivo della programmazione Java, per il momento a prescindere da Codename One. Vediamo passo dopo passo come poter risolvere questo problema.
Codice iniziale
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
}
}
Output:
Calcolo spazio percorso da un'automobile
Il senso di questo codice è quello appunto di mostrare la stringa di testo riportata in output. Per il momento e per gli scopi di questo paragrafo non mi interessa commentare nello specifico il significato di ogni parola che compone questo codice. A grandi linee, possiamo ragionare così:
-
public class MyClass { ... } è la classe principale, ovvero quella che viene richiamata per prima, a cui viene affidato il compito di far partire il programma (descriverò più avanti che cosa è una classe);
-
public static void main(String args[]) { ... } è il metodo principale di tale classe, di nome "main" (descriverò più avanti cosa è un metodo);
-
System.out.println("xxx") serve per mostrare in output ciò che è contenuto tra i doppi apici, in questo caso xxx.
Andiamo avanti, abbiamo detto che ci serve un algoritmo per calcolare lo spazio, conoscendo la velocità e il tempo.
Codice con l'aggiunta di un metodo per il calcolo dello spazio
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
}
/**
* Applica la formula spazio = velocita * tempo
*
* @param velocita in metri al secondo
* @param tempo in secondi
* @return spazio in metri
*
*/
private float spazio (float velocita, float tempo) {
return velocita * tempo;
}
}
L'aggiunta di codice è autoesplicativa: il metodo private float spazio (float velocita, float tempo) { ... } è commentato dal Javadoc che lo precede, quello che inizia con /** e termina con */. In sintesi, il metodo si chiama "spazio", prende in input i parametri di tipo float "velocita" e "tempo" e restituisce in output un numero che rappresenta lo spazio: "float" significa numero con virgola, ad es. il numero "3.14" (il punto rappresenta la virgola) è un float. Sto semplificando, vedremo più avanti i vari tipi di valori numerici che possono essere passati a un metodo.
A questo punto, dovrebbe essere evidente che il concetto di metodo di una classe (in questo caso il metodo "spazio") è concettualmente molto simile al concetto matematico di funzione.
Per risolvere il nostro problema, notiamo che il metodo "spazio" richiede che i valori di velocità e tempo siano specificati in unità di misura diverse rispetto a quelle dei dati forniti. Nello specifico, la velocità è in km/h e il tempo è in minuti. Allora ci servono altri due metodi per convertire queste unità di misura in quelle volute. Il nostro codice diventa:
Codice con l'aggiunta dei metodi per la conversione delle unità di misura
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
}
/**
* Applica la formula spazio = velocita * tempo
*
* @param velocita in metri al secondo
* @param tempo in secondi
* @return spazio in metri
*
*/
private float spazio (float velocita, float tempo) {
return velocita * tempo;
}
/**
* Converte km/h in m/s
*
* @param kmh velocita in km/h
* @return velocita in m/s
*
*/
private float ms (float kmh) {
return kmh / 3.6f;
}
/**
* Converte minuti in secondi
*
* @param min minuti
* @return secondi
*
*/
private int sec (int min) {
return min * 60;
}
}
Nell'ultimo metodo, la parola "int" significa "numero intero", cioè senza virgola. Nel penultimo metodo, la "f" attacca a "3.6" significa che tale numero deve essere interpretato come un float (dettaglio su cui per il momento non entro).
Infine, nel metodo principale "main", inseriamo l'algoritmo risolutivo del nostro problema, che a sua volta sfrutta gli algoritmi appena creati:
Codice completo risolutivo del nostro problema
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
// dati del problema
int v = 108; // km/h
int t = 10; // minuti
float v_ms = ms(v); // prende v in km/h e lo converte in m/s
float t_s = sec(t); // prende t in minuti e lo converte in secondi
float risultato = spazio(v_ms, t_s); // calcola lo spazio
// output
System.out.println("Risultato: " + risultato + " metri");
}
/**
* Applica la formula spazio = velocita * tempo
*
* @param velocita in metri al secondo
* @param tempo in secondi
* @return spazio in metri
*
*/
private static float spazio (float velocita, float tempo) {
return velocita * tempo;
}
/**
* Converte km/h in m/s
*
* @param kmh velocita in km/h
* @return velocita in m/s
*
*/
private static float ms (float kmh) {
return kmh / 3.6f;
}
/**
* Converte minuti in secondi
*
* @param min minuti
* @return secondi
*
*/
private static int sec (int min) {
return min * 60;
}
}
Output:
Calcolo spazio percorso da un'automobile Risultato: 18000.0 metri
Al di là di tutti i dettagli implementativi e delle parole specifiche del linguaggio Java (per completare il codice, ho aggiunto la parola "static" a tutti i metodi, ma è prematuro spiegarne il perché), l'importante è iniziare a vedere un parallelismo tra quella che è la risoluzione di un problema molto semplice e la sua scomposizione in algoritmi.
Il codice di esempio sopra riportato può essere copiato, incollato ed eseguito alla pagina https://www.jdoodle.com/online-java-compiler/, ottenendo lo stesso output. Chi vuole può provare a modificare il codice, ad es. cambiando i dati, per vedere come cambia l'output.
Per ogni dubbio di natura matematica sulla risoluzione di questo specifico problema, il suo svolgimento in maniera classica, cioè come si farebbe a scuola, è riportato integralmente e commentato a questa pagina: https://www.chimica-online.it/test-fisica/svolgimento/esercizio-moto-rettilineo-uniforme-1.htm
Visto che sono partito dalla matematica per arrivare agli algoritmi, adesso vorrei fare un discorso più generale. In base alla mia esperienza, ritengo che le conoscenze matematiche richieste per lo sviluppo di applicazioni per smartphone, nella stragrande maggioranza dei casi, siano quelle dell’algebra elementare, della geometria cartesiana di base, della risoluzione di proporzioni. Raramente mi è capitata una matematica ben più impegnativa, perché, quando mi è stata necessaria, ho trovato strumenti già pronti per la risoluzione di problemi specifici, ovvero codice condiviso in rete da altri sviluppatori, o integrato in apposite librerie. Ad es., sebbene la sola gestione delle comunicazioni protette con criptografia sia matematicamente complessa (per capirci, tutte le comunicazioni di rete che iniziano con protocollo “https”), di norma l’ambiente di sviluppo ne integra già la gestione automatica. Stesso discorso per il calcolo degli hash, per il quale esistono apposite librerie. A volte può capitare di dover usare la trigonometria per gestire il movimento di oggetti: di per sé non richiede un sforzo eccessivamente complicato, visto che in Rete si trovano tutti i formulari; al massimo, l’unica complicazione è tenere a mente che l’ordinata va dall’alto verso il basso e non dal basso verso l’alto (come invece abbiamo imparato a scuola). Quando avremo bisogno di scrivere algoritmi sul piano cartesiano dello schermo dello smartphone, ascissa e ordinata sono così disposte:
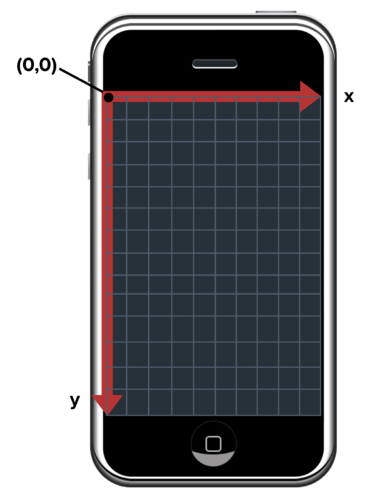
Non disponiamo dell'asse z, che servirebbe per passare dal piano cartesiano allo spazio euclideo tridimensionale, però possiamo usare uno z-index per organizzare l'ordine di sovrapposizione di elementi sovrapposti sullo stesso piano.
Algoritmi in funzione degli strumenti di cui disponiamo e della logica del linguaggio di programmazione
Per pensare gli algoritmi, prima ancora di tentare di scriverli, dobbiamo sapere di quali strumenti disponiamo. Ogni linguaggio di programmazione ha la sua logica, i suoi limiti e i suoi punti di forza, è predisposto per agevolare un certo modo di ragionare per ostacolare altre modalità. In altre parole, ogni linguaggio ha il suo modus cogitandi e modus operandi.
Nel nostro caso, non useremo tutte le possibilità di Java, ma solo quel suo sottoinsieme minimo richiesto da Codename One. Nello specifico, si tratta di Java 5 con l'aggiunta di alcune funzionalità di Java 8. Il fatto di usare Codename One con versioni di Java successive alla 8 (nel momento in cui scrivo Java è arrivato alla versione 13) non dà alcun vantaggio, nel senso che comunque non potremo usare le funzionalità di Java non supportate da Codename One.
Detto ancora più esplicitamente, soprattutto per coloro che già non conoscono Java, le caratteristiche da studiare e da usare di Java sono quelle di Java 5 e alcune di Java 8. Nel prossimo articolo indicherò più dettagliatamente a quale documentazione far riferimento, intanto segnalo un manuale gratuito, liberamente ridistribuibile, di Java 5: "Claudio De Sio Cesari - Manuale di Java 5". Lo stesso autore ha pubblicato anche un valido manuale di Java 8, usato sia nel mondo del lavoro sia nei corsi universitari: si trova abbastanza facilmente in rete (sia come epub sia come pdf), però io non posso redistribuirlo per motivi di copyright dell'editore.
Sebbene questa caratteristica di Codename One di supportare un sottoinsieme di Java sembri una limitazione, in realtà è un punto di forza per la sua compatibilità multipiattaforma, come spiegato nell'articolo Why we don't Support the Full Java API. Tra l'altro, nonostante Codename One funzioni con una versione di Java ormai iper-collaudata e stabile, per non dire vecchia (nel momento in cui scrivo, comunque, Java 8 continua a ricevere aggiornamenti da Oracle), dall'altra le app con esso prodotte sono sempre adeguate agli ultimi standard imposti da Google e da Apple. E' possibile comunque usare Codename One anche con Java 11, ma non con altre versioni di Java (il motivo è spiegato in questo commento su Stack Overflow). Darò poi indicazioni pratiche su come creare il proprio ambiente di sviluppo nel prossimo articolo.
Ciò premesso, una regola generale è che, quando ci serve una funzionalità non offerta dal linguaggio di programmazione che stiamo usando, possiamo:
- crearcela da soli, sfruttando con creatività le funzionalità di cui già disponiamo;
- cercare in rete esempi di codice o tutorial che riguardano proprio ciò di cui abbiamo bisogno;
- cercare librerie (nel nostro caso CN1Libs) che implementano ciò di cui abbiamo bisogno;
- chiedere consigli a sviluppatori su esperti, ad es. sulla piattaforma di mutuo aiuto Stack Overflow.
Facciamo un esempio pratico. Supponiamo di utilizzare un linguaggio di programmazione nel quale non esistono i classici operatori matematici per eseguire le quattro operazioni di base, ma soltanto operatori di incremento e decremento di un numero: come facciamo a risolvere lo stesso problema, precedentemente affrontato, del calcolo dello spazio percorso da un'automobile che si muove secondo le leggi del moto rettilineo uniforme? Per semplicità, stavolta suppongo che i dati del problema siano già nelle unità di misura corrette. Ecco una possibile soluzione, sotto commentata:
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
// dati del problema
int v = 30; // metri al secondo
int t = 10; // secondi
float risultato = spazio(v, t); // calcola lo spazio
// output
System.out.println("Risultato: " + risultato + " metri");
}
/**
* Applica la formula spazio = velocita * tempo
*
* @param velocita in metri al secondo
* @param tempo in secondi
* @return spazio in metri
*
*/
private static int spazio (int velocita, int tempo) {
return velocita * tempo;
}
/**
* Somma due numeri, usando esclusivamente
* l'operatore di incremento ++
* e l'operatore di decremento --
*
* @param kmh velocita in km/h
* @return velocita in m/s
*
*/
private static int somma (int a, int b) {
if (b == 0) {
return a;
} else {
return somma(a++, b--);
}
}
/**
* Moltiplica due numeri, senza usare l'operatore
* di moltiplicazione, ma esclusivamente il metodo
* "somma" precedentemente creato
*
*/
private static int moltiplica (int a, int b) {
if (b == 0) {
return 0;
} else if (b == 1) {
return a;
} else {
return moltiplica(somma(a,a), b--);
}
}
}
Output:
Calcolo spazio percorso da un'automobile Risultato: 300.0 metri
Anche in questo caso, il codice da me proposto può essere provato su https://www.jdoodle.com/online-java-compiler/
Ciò che ho fatto è stata la creazione di un metodo ricorsivo che esegue una somma tramite incrementi e di un altro metodo ricorsivo che esegue una moltiplicazione tramite somme. Tramite questo stratagemma matematico, più o meno simile a come risolvevamo i problemi in prima elementare quando ancora non conoscevamo le moltiplicazioni e quando ancora facevamo le addizioni con le dita, ho raggirato una limitazione che, per scopo didattico, mi sono autoimposto.
Il codice dovrebbe essere autoesplicativo. Il flusso di esecuzione, in entrambi gli algoritmi ricorsivi, è affidato a un costrutto condizionale if... else if... else, che vuol dire: se si verifica la tale condizione fai questo, altrimenti fai quest'altro. Poi vedremo con maggiore dettaglio la sintassi di questo costrutto.
Per completezza, e in maniera peraltro più efficiente (in quanto usa meno memoria), lo stesso codice di prima può essere riscritto tramite algoritmi non ricorsivi, usando i cicli for, che per ora mostro senza ulteriori spiegazioni:
public class MyClass {
public static void main(String args[]) {
System.out.println("Calcolo spazio percorso da un'automobile");
// dati del problema
int v = 30; // metri al secondo
int t = 10; // secondi
float risultato = spazio(v, t); // calcola lo spazio
// output
System.out.println("Risultato: " + risultato + " metri");
}
/**
* Applica la formula spazio = velocita * tempo
*
* @param velocita in metri al secondo
* @param tempo in secondi
* @return spazio in metri
*
*/
private static int spazio (int velocita, int tempo) {
return velocita * tempo;
}
/**
* Somma due numeri, usando esclusivamente
* l'operatore di incremento ++
* e l'operatore di decremento --
*
* @param kmh velocita in km/h
* @return velocita in m/s
*
*/
private static int somma (int a, int b) {
int risultato = a;
for (int i=0; i<b; i++){
risultato++;
};
return risultato;
}
/**
* Moltiplica due numeri, senza usare l'operatore
* di moltiplicazione, ma esclusivamente il metodo
* "somma" precedentemente creato
*
*/
private static int moltiplica (int a, int b) {
if (b == 0) return 0;
int risultato = a;
for (int i=1; i<b; i++){
risultato = somma(risultato, a);
};
return risultato;
}
}
Anche in questo caso l'output, verificabile con l'online compiler, è:
Calcolo spazio percorso da un'automobile Risultato: 300.0 metri
Questi esempi mostrano come un po' di astrazione matematica sia sicuramente utile.
Nel prossimo articolo, che sarà la terza parte della sezione dedicata agli algoritmi, vedremo più in dettaglio quale documentazione prendere come riferimento, sia relativamente a Java sia a Codename One, vedremo quali sono gli strumenti software, hardware e cloud che ci servono per sviluppare app multipiattaforma e, continuando con un esempi minimali in Java, faremo la nostra prima app.
Francesco Galgani,
13 dicembre 2019
